动态规划套路

509. 斐波那契数 (opens new window)

322. 零钱兑换 (opens new window)

动态规划这类问题一般形式就是求最值。而求最值的核心问题就是穷举。因为只要知道所有的情况，然后在其中找到最值即可。

只要是最值就要想着最值的问题。

动态规划这类问题存在三大要素：

• 重叠子问题
• 最优子结构
• 正确的'状态转移方程'

斐波那契数

题目：

思想：

这题是一道比较简单又比较经典的问题，更是一个递归的好应用：

class Solution {
    public int fib(int n) {
        if (n == 0) {
            return 0;
        }
        if (n == 2 || n == 1) {
            return 1;
        } 
        return fib(n - 1) + fib(n - 2);
    }
}

但是这种递归效率特别低，比如当求N=20，则需求N=18,N=19,而当N=21，则需求N=20,N=19,可以看到N=19，被多次计算，这就是所谓的重叠子问题

优化：

重叠子问题：穷举一般来说效率比较低下，比如要从100个数中找到最小的数字，一个一个比较，就有太多不必要的计算了，所以重叠子问题主要就是避免不必要的计算。

既然存在太多不必要的计算，我们优化的方式当然就是避免这些不必要的计算。

优化1-备忘录：

我们每次记录下某个子问题的答案，当遇到这个子问题的时候就去备忘录中查询并返回，如果没有这个子问题，就求出这个子问题并记录。

class Solution {
    public int fib(int n) {
        if(n == 0) return 0;
        int[] nums = new int[n + 1]; 
        return helper(nums, n);
    }
    int helper(int[] nums, int n) {
        if (n == 1 || n == 2) return 1;
        if(nums[n] != 0) {
            return nums[n];
        }
        nums[n] = helper(nums, n - 1) + helper(nums, n - 2);
        return nums[n];
    }
}

优化2-dp

备忘录的方法实质上还是递归，这是我们避免了在递归中计算已经计算过的子问题。

优化1是自顶向下的，现在我们来实现自底向上。

class Solution {
    public int fib(int n) {
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;
        int[] nums = new int[n + 1];
        nums[1] = nums[2] = 1;
        for(int i = 3; i <= n; i++) {
            nums[i] = nums[i - 1] + nums[i - 2];
        }
        return nums[n];
    }
}

通过自底向上的实现，大致能总结出一个规律：

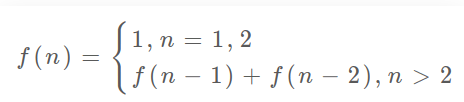
而这个就是我们的状态转移方程。

套路：

• 使用暴力解法得到状态转移方程
• 利用备忘录和DP table优化暴力解法

最终代码：

class Solution {
    public int fib(int n) {
        if (n == 0) {
            return 0;
        }
        if (n == 2 || n == 1) {
            return 1;
        } 
        int pre = 1, next = 1;
        for(int i = 3; i <= n; i++) {
            int sum = pre + next;
            pre = next;
            next = sum;
        }
        return next;
    }
}

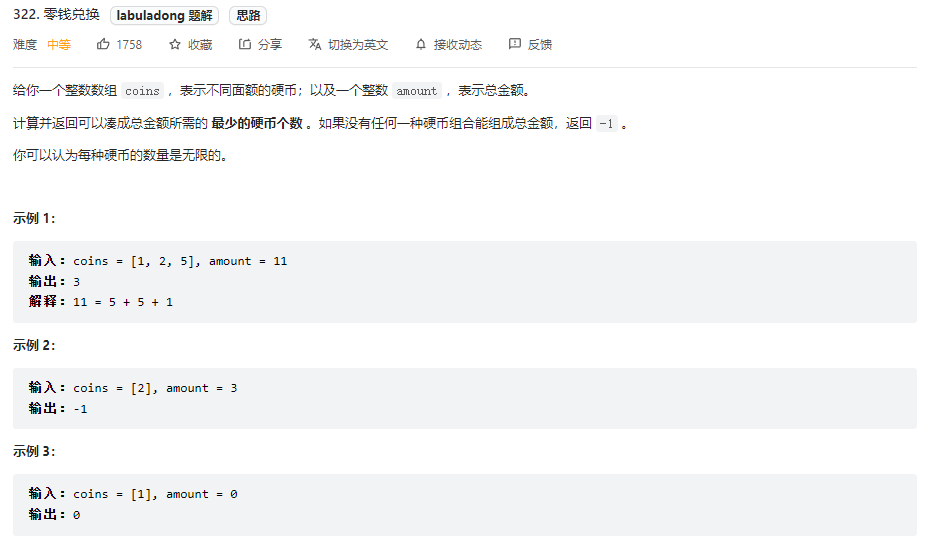
零钱兑换

题目：

思想：

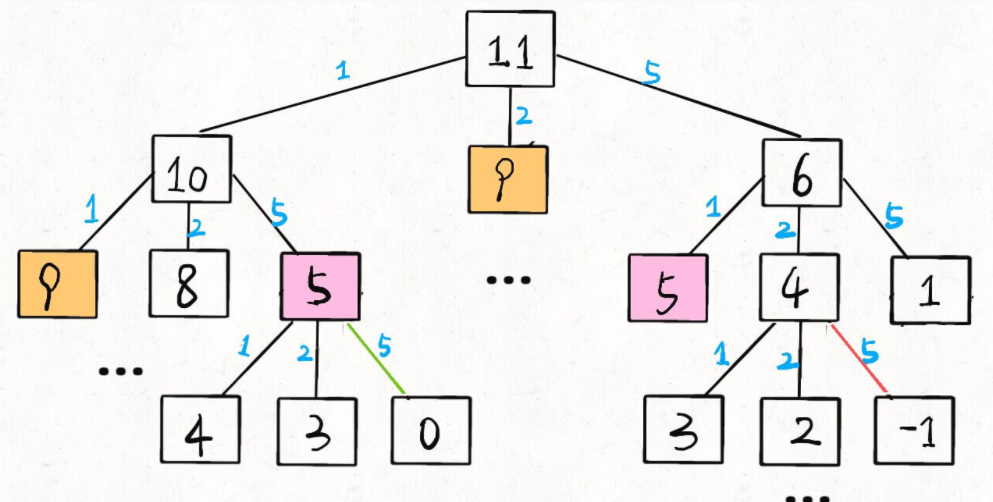
代码：

class Solution {
    int[] memo;

    public int coinChange(int[] coins, int amount) {
        memo = new int[amount + 1];
        // dp 数组全都初始化为特殊值,为特殊值说明此刻拼凑amount数量的问题还没有解
        Arrays.fill(memo, -10);
        return dp(coins, amount);
    }

    int dp(int[] coins, int amount) {
        if (amount == 0) return 0;
        if (amount < 0) return -1;
        // 防止重复计算
        if (memo[amount] != -10)
            return memo[amount];
        int res = Integer.MAX_VALUE;
        for (int coin : coins) {
            // 计算子问题的结果，减去coin，相当于少用一枚硬币
            int subProblem = dp(coins, amount - coin);
            // 子问题无解则跳过
            if (subProblem == -1) continue;
            // 在子问题中选择最优解，然后加一
            res = Math.min(res, subProblem + 1);
        }
        // 把计算结果存入备忘录
        memo[amount] = (res == Integer.MAX_VALUE) ? -1 : res;
        return memo[amount];
    }
}

参考

动态规划解题套路框架 (opens new window)