 回溯算法套路
回溯算法套路
# 回溯算法套路
解决一个回溯问题,实际上就是一个决策树的遍历过程中。
决策树:是在已知各种情况发生概率的基础 (opens new window)上,通过构成决策树来求取净现值的期望 (opens new window)值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。
说得简单一点就是你会面临多种情况,这些多种情况的组合就是决策树。而决策树有三个重点:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
框架:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
题目:
# 全排列问题
题目:
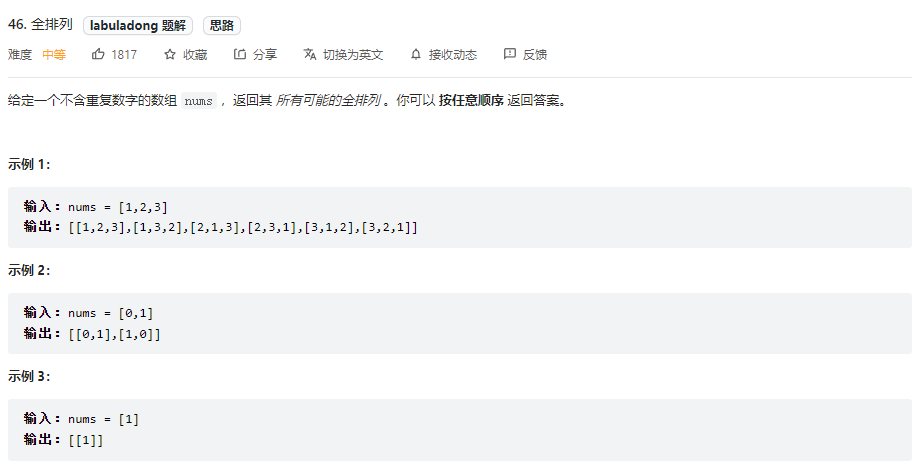
思想:
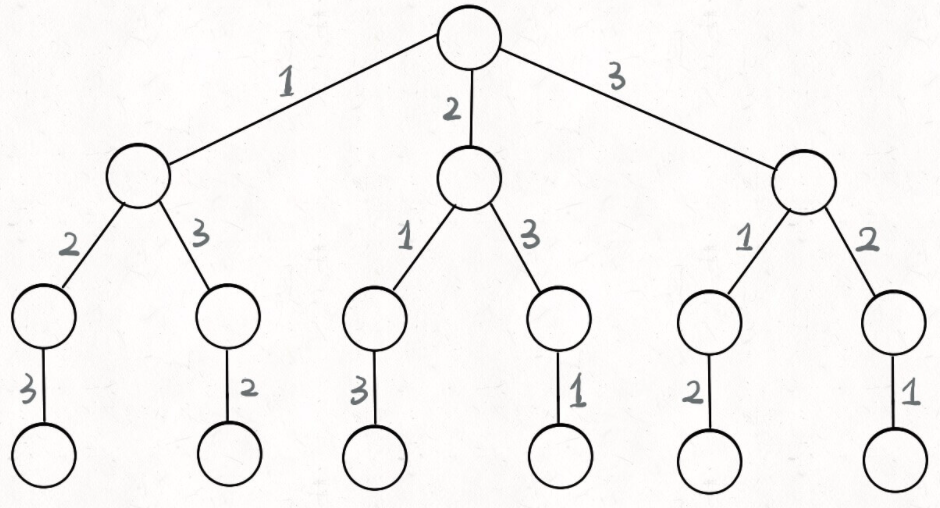
比如在第一个头结点,可以选择有三个节点(1,2,3),而此时我的路径为空;当选择1的时候,这时候路径为(1),而此刻选择变成了两个节点(2和3);当又选择2的时候,这时候路径为(1,2),而此刻选择只有3,当选择3的时候,这时候路径为(1,2,3),而现在结束条件已经满足,结束这次选择。
代码:
class Solution {
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
// 用于存放选择路径
List<Integer> track = new ArrayList<>();
backTrack(nums, track);
return result;
}
void backTrack(int[] nums, List<Integer> track) {
// 满足结束条件
if(track.size() == nums.length) {
// 添加路径
result.add(new ArrayList<>(track));
return;
}
for(int i = 0; i < nums.length; i++) {
// 排除已经选择过的
if(track.contains(nums[i])) {
continue;
}
// 添加选择
track.add(nums[i]);
// 递归
backTrack(nums, track);
// 撤销选择
track.remove(track.size() - 1);
}
}
}
# N皇后问题
题目:

思想:
这次可以选择的列表相当于是一个二维数组,可以在二维数组的任何地方下棋,然后结束条件是当每一行都下棋了,说明已经结束了。排除已经选择的则是你所下棋的位置有限制。
选择列表:
char[][] board = new char[n][n];
for (char[] c : board) {
Arrays.fill(c, '.');
}
结束条件:
// 满足结束条件
if (row == board.length) {
result.add(charToList(board));
return;
}
排除已经选择的:
public Boolean isValid(char[][] board, int row, int col) {
int n = board.length;
// 检查列
for (int i = 0; i < n; i++) {
if (board[i][col] == 'Q') {
return false;
}
}
// 检查右上方是否有皇后冲突
for (int i = row - 1, j = col + 1; i >=0 && j < n; i--, j++) {
if (board[i][j] == 'Q') {
return false;
}
}
// 检查左上方是否有皇后冲突
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q') {
return false;
}
}
return true;
}
代码:
public class Solution {
List<List<String>> result = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
// "." 表示空,"Q"表示皇后,初始化棋盘,就是选择列表
char[][] board = new char[n][n];
for (char[] c : board) {
Arrays.fill(c, '.');
}
backTrack(board, 0);
return result;
}
void backTrack(char[][] board, int row) {
// 满足结束条件
if (row == board.length) {
result.add(charToList(board));
return;
}
for (int col = 0; col < board.length; col++) {
// 排除可以相互攻击的格子
if (!isValid(board, row, col)) {
continue;
}
// 做选择
board[row][col] = 'Q';
// 递归
backTrack(board, row + 1);
// 撤销选择
board[row][col] = '.';
}
}
public List<String> charToList(char[][] board) {
List<String> list = new ArrayList<>();
for (char[] temp : board) {
list.add(String.copyValueOf(temp));
}
return list;
}
public Boolean isValid(char[][] board, int row, int col) {
int n = board.length;
// 检查列
for (int i = 0; i < n; i++) {
if (board[i][col] == 'Q') {
return false;
}
}
// 检查右上方是否有皇后冲突
for (int i = row - 1, j = col + 1; i >=0 && j < n; i--, j++) {
if (board[i][j] == 'Q') {
return false;
}
}
// 检查左上方是否有皇后冲突
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q') {
return false;
}
}
return true;
}
}
# 参考
上次更新: 2024/06/29, 15:13:44
